The foundations of the computational method for determining if a point lies within the boundaries of a 2 dimensional polygon, relies on the concept of counting how many times a ray intersects within the boundary of the polygon. If the count of the number of times a ray intersects a polygon is odd, than the point lies within the polygon.
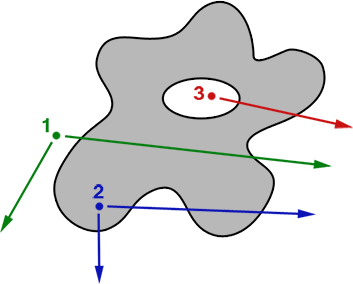
We can solve this problem computationally by running a semi-infinite ray horizontally (by increasing x and keeping y fixed) within a array of coordinates that make up a Jordan curve theorem polygon. W. Randolph Franklin was one of the early programmers to solve the problem within the programing language FORTRAN and C with only 7 lines of code called PNPoly.
int pnpoly(int numberOfVertices,
float *verticesX, float *verticesY,
float textPointX, float textPointY)
{
int i, j, c = 0;
for (i = 0, j = numberOfVertices-1; i < numberOfVertices; j = i++) {
if (
( (verticesY[i]>textPointY) != (verticesY[j]>textPointY) )
&& ( textPointX < (verticesX[j]-verticesX[i])
* (textPointY-verticesY[i])
/ (verticesY[j]-vertY[i]) + verticesX[i]) )
c = !c;
}
return c;
}Similarly we can apply this to a javascript method to handle a point as an array of x & y, and polygon as an array of coordinates on a grid. We can also add handling for a point existing on the boundary of a polygon.
pnpoly = function (point, polygon) {
var x = point[0], y = point[1];
var inside = false;
for (var i = 0, j = polygon.length - 1; i < polygon.length; j = i++) {
var xi = polygon[i][0], yi = polygon[i][1];
var xj = polygon[j][0], yj = polygon[j][1];
if (yi == yj && yi == y && x > min(xi, xj) && x < max(xi, xj)) {
// Check if point is on an horizontal polygon boundary
return true;
}
var xinters = (y - yi) * (xj - xi) / (yj] - yi) + xi;
if (xinters == x) {
// Check if point is on the polygon boundary (other than horizontal)
return true;
}
var intersect = ((yi > y) != (yj > y))
&& (x < (xj - xi) * (y - yi) / (yj - yi) + xi);
if (intersect) inside = !inside;
}
return inside;
};